EWASG#

Thermophysical Properties#

The EWASG (WAter-Salt-Gas) fluid property module was developed by Battistelli et al., 1997 for modeling geothermal reservoirs with saline fluids and non-condensible gas (NCG). In contrast to EOS7, EWASG describes aqueous fluid of variable salinity not as a mixture of water and brine, but as a mixture of water and NaCl. This makes it possible to represent temperature-dependent solubility constraints, and to properly describe precipitation and dissolution of salt. EWASG represents the active system components (water, NaCl, NCG) as three-phase mixtures. Solid salt is the only active mineral phase, and is treated in complete analogy to fluid phases (aqueous, gas), except that, being immobile, its relative permeability is identically zero. From mass balances on salt in fluid and solid phases we calculate the volume fraction of precipitated salt in the original pore space \(\phi_0\), which is termed “solid saturation”, and denoted by \(S_s\). A fraction \(\phi_0 S_s\) of reservoir volume is occupied by precipitate, while the remaining void space \(\phi_f = \phi_0 \left( 1 - S_s \right)\) is available for fluid phases. We refer to \(\phi_f\) as the “active flow porosity”. The reduction in pore space reduces the permeability of the medium.

Several choices are available for the non-condensible gas (NCG): CO₂, air, CH₄, H₂, and N₂. Gas dissolution in the aqueous phase is described by Henry’s law, with coefficients that depend not only on temperature but also on salinity to describe the reduction in NCG solubility with increasing salinity (“salting out”). The dependence of brine density, enthalpy, viscosity, and vapor pressure on salinity is taken into account, as are vapor pressure-lowering effects from suction pressures (capillary and vapor adsorption effects). The thermophysical property correlations used in EWASG are accurate for most conditions of interest in geothermal reservoir studies: temperatures in the range from 100 to 350˚C, fluid pressures up to 80 MPa, CO₂ partial pressures up to 10 MPa, and salt mass fraction up to halite saturation. With the exception of brine enthalpy, thermophysical property correlations are accurate to below 10˚C. A full discussion of the thermophysical property correlations used and their empirical basis is given in the original paper (Battistelli et al., 1997).

TOUGH3 also adopts recent improvements of EWASG. Internally consistent correlations for the water-NaCl mixture properties are included (Battistelli, 2012), which are developed by Driesner & Heinrich, 2007 and Driesner, 2007. These brine correlations are capable to calculate phase properties for temperatures from 0 to 350˚C, pressures from 1 to 100 MPa, and salt mass fraction up to saturation. In TOUGH3, the brine correlations in Driesner, 2007 are used as the default, unless specified differently by users.

New options are also added to calculate NCG (CO₂, CH₄, and H₂ only) density and fugacity using a virial equation treatment of Spycher & Reed, 1988. This method is available and reliable only for the following temperature and pressure ranges: (1) for CO₂, 50 - 350˚C and up to 50 MPa, (2) for CH₄, 16 - 350˚C and up to 50 MPa, and (3) for H₂, 25 - 600˚C and up to 300 MPa.

Permeability Change#

As noted above, the relationship between the amount of solid precipitation and the pore space available to the fluid phases is very simple. The impact of porosity change on formation permeability on the other hand is highly complex. Laboratory experiments have shown that modest reductions in porosity from chemical precipitation can cause large reductions in permeability (Vaughn, 1987). This is explained by the convergent-divergent nature of natural pore channels, where pore throats can become clogged by precipitation while disconnected void spaces remain in the pore bodies (Verma & Pruess, 1988). The permeability reduction effects depend not only on the overall reduction of porosity but on details of the pore space geometry and the distribution of precipitate within the pore space. These may be quite different for different porous media, which makes it difficult to achieve generally applicable, reliable predictions. EWASG offers several choices for the functional dependence of relative change in permeability, \(\frac{k}{k_0}\), on relative change in active flow porosity.

(70)#\[\frac{k}{k_0} = f \left( \frac{\phi_f}{\phi_0} \right) \equiv f \left( 1 - S_s \right)\]

The simplest model that can capture the converging-diverging nature of natural pore channels consists of alternating segments of capillary tubes with larger and smaller radii, respectively; see Figure 8. While in straight capillary tube models permeability remains finite as long as porosity is non-zero, in models of tubes with different radii in series, permeability is reduced to zero at a finite porosity.

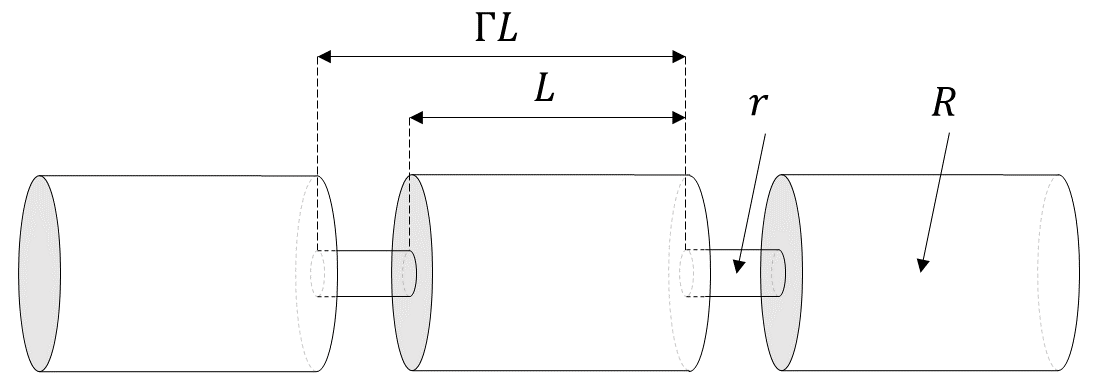
Conceptual model — Figure 8 Model for converging-diverging pore channels.#

From the tubes-in-series model shown in Figure 8, the following relationship can be derived (Verma and Pruess, 1988)

(71)#\[\frac{k}{k_0} = \theta^2 \frac{1 - \Gamma + \frac{\Gamma}{\omega^2}}{1 - \Gamma + \Gamma \left( \frac{\theta}{\theta + \omega - 1} \right)^2}\]

Here

(72)#\[\theta = \frac{1 - S_s - \phi_r}{1 - \phi_r}\]

depends on the fraction \(1 - S_s\) of original pore space that remains available to fluids, and on a parameter \(\phi_r\), which denotes the fraction of original porosity at which permeability is reduced to zero. \(\Gamma\) is the fractional length of the pore bodies, and the parameter \(\omega\) is given by

(73)#\[\omega = 1 + \frac{\frac{1}{\Gamma}}{\frac{1}{\phi_r} - 1}\]

Therefore, Eq. (71) has only two independent geometric parameters that need to be specified, \(\phi_r\) and \(\Gamma\). As an example, Figure 9 shows the permeability reduction factor from Eq. (71), plotted against \(\frac{\phi}{\phi_0} \equiv \left( 1 - S_s \right)\), for parameters of \(\phi_r\) = \(\Gamma\) = 0.8.

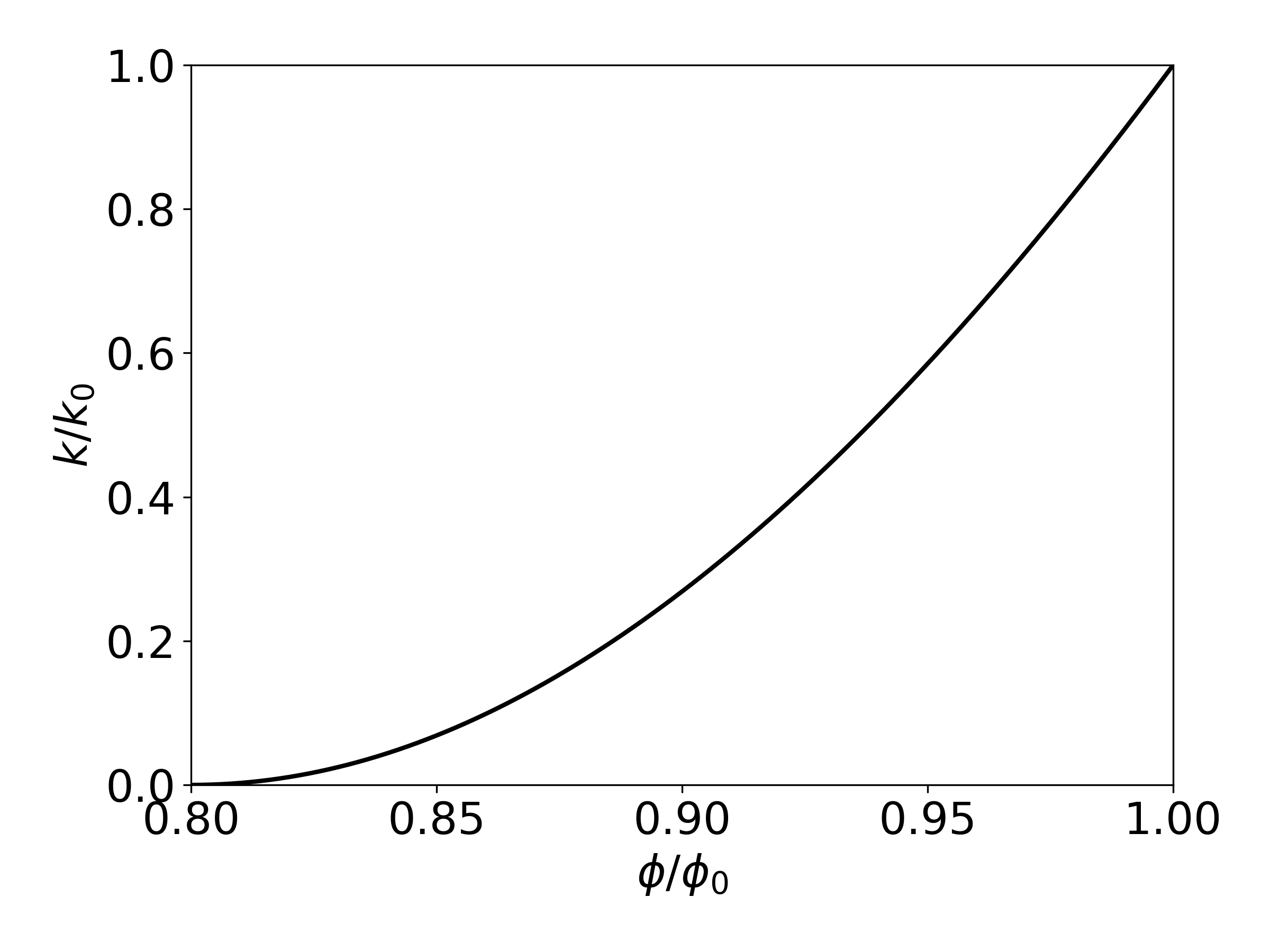
../../_images/porosity_permeability.png — Figure 9 Porosity-permeability relationship for tubes-in-series model, after Verma & Pruess, 1988.#

For parallel-plate fracture segments of different aperture in series, a relationship similar to Eq. (71) is obtained, the only difference being that the exponent 2 is replaced everywhere by 3 (Verma & Pruess, 1988). If only straight capillary tubes of uniform radius are considered, we have \(\phi_r\) = 0, \(\Gamma\) = 0, and Eq. (71) simplifies to

(74)#\[\frac{k}{k_0} = \left( 1 - S_s \right)^2\]

Specifications#

A summary of EWASG specifications and parameters appears in Table 97. The default parameter settings are (NK, NEQ, NPH, NB) = (3, 4, 3, 6). The NK = 2 (no air) option may only be used for problems with single-phase liquid conditions throughout. The primary variables are (\(P\), \(X_{sm}\), \(X3\), \(T\)) for single-phase conditions and (\(P\), \(X_{sm}\), \(S_g\) + 10, \(T\)) for two-phase conditions.

Primary variable #2 (\(X2\)) is used for NaCl, and denotes mass fraction \(X_s\) in the aqueous phase when no solid salt is present, while it is solid saturation plus ten (\(S_s\) + 10) in the presence of precipitated salt. The number 10 is added here to be able to determine whether or not a precipitated phase is present from the numerical range of the second primary variable. Solubility of NaCl in the gas phase is very small at the pressure and temperature conditions considered for EWASG and has been neglected. During the Newton-Raphson iteration process, possible appearance or disappearance of a solid phase is checked, as follows. If no solid phase was present at the previous iteration, primary variable \(X2\) is known to denote salt mass fraction \(X_s\) in the aqueous phase, and the latest updated value is compared with the equilibrium solubility \(XEQ\). If \(S_s\) > \(XEQ\), precipitation starts, a small solid phase saturation is initialized as \(S_s\) = 10^-6, and the second primary variable is switched to \(X2\) = \(S_s\) + 10. If solid salt had been present at the previous iteration, EWASG checks whether \(S_s\) = \(X2\) - 10 is still larger than 0. If not, this indicates that the solid phase disappears; the second primary variable is then switched to dissolved salt mass fraction, and is initialized just below equilibrium solubility as \(S_s\) = \(XEQ\) - 10^-6.

Table 97 Summary of EWASG.#
Components	#1: water #2: NaCl #3: NCG (CO₂, air, CH₄, H₂, N₂; optional)
Parameter choices	(`NK`, `NEQ`, `NPH`, `NB`) = (3, 4, 3, 6) water, NaCl, NCG, nonisothermal (default) (3, 3, 3, 6) water, NaCl, NCG, isothermal (2, 3, 2, 6) water, NaCl, nonisothermal* (2, 2, 2, 6) water, NaCl, isothermal* Molecular diffusion can be modeled by setting `NB` = 8
Primary variables	Single-phase conditions (only liquid or only gas): (\(P\), \(X_{sm}\), \(X3\), \(T\)): (pressure, salt mass fraction or solid saturation plus ten, NCG mass fraction, temperature) Two-phase conditions: (\(P\), \(X_{sm}\), \(S_g\) + 10, \(T\)): (pressure, salt mass fraction or solid saturation plus ten, gas phase saturation plus ten, temperature)

Note

* the NK = 2 (no NCG) option may only be used for problems with single-phase liquid conditions throughout.

† two-phase conditions may be initialized with variables (\(T\), \(X_{sm}\), \(S_g\) + 10, \(P_{NCG}\)), or (\(T\), \(X_{sm}\), \(S_g\) + 10, \(X3\)), where \(P_{NCG}\) is the partial pressure of NCG, \(X3\) is mass fraction of NCG in the liquid phase; by convention, EWASG will assume the first primary variable to be pressure if it is larger than 370, otherwise it will be taken to be temperature; if the first primary variable is temperature, the last primary variable will be taken to mean mass fraction of NCG if it is less than 1, otherwise it will be taken to mean NCG partial pressure.

Selections#

Various options for EWASG can be selected through parameter specifications in data block SELEC, as follows

Table 98 Record **SELEC.1**.#
Parameter	Format	Description
`IE(1)`	I5	set equal to 1, to read one additional data record (a larger value with more data records is acceptable, but only one additional record will be used by EWASG).
`IE(3)`	I5	allows choice of brine viscosity calculation: 0: after Phillips et al. (1981) (default). 1: after Palliser and McKibbin (1998). 2: after Mao and Sun (2006). 3: after Potter (1978).
`IE(4)`	I5	allows choice of correlation for compressed brine density: 1: after Andersen et al. (1992) (default = 0). 2: Pritchett (1993). 3: Brine compressibility equal to water compressibility at the same reduced temperature. 4: Brine compressibility equal to water compressibility at the same temperature. 5: after Batzle and Wang (1992). 6: after Driesner (2007).
`IE(8)`	I5	allows choice of NCG density and fugacity calculation: 0: original EWASG approach (default). 1: NCG density according to Spycher and Reed (1988). Only for CO₂, CH₄, and H₂. 2: NCG density and gas-aqueous equilibrium according to Spycher and Reed (1988). Only for CO₂, CH₄, and H₂.
`IE(9)`	I5	allows choice of NCG enthalpy calculation in the aqueous phase: 0: original EWASG approach (default). 1: NCG enthalpy as a function of temperature.
`IE(10)`	I5	allows to turn vapor pressure lowering on/off: 0: VPL is off. 1: VPL is on.
`IE(11)`	I5	selects dependence of permeability on the fraction \(\frac{\phi_f}{\phi_0} = \left( 1 - S_s \right)\) of original pore space that remains available to fluids: 0: permeability does not vary with \(\phi_f\). 1: \(\frac{k}{k_0} = \left( 1 - S_s \right)^{\gamma}\), with \(\gamma\) = `FE(1)`. 2: fractures in series, i.e., Eq. (71) with exponent 2 everywhere replaced by 3. 3: tubes-in-series, i.e., Eq. (71).
`IE(14)`	I5	allows choice of treatment of thermophysical properties as a function of salinity: 0: full dependence (default). 1: vapor pressure independent of salinity. 2: vapor pressure and brine enthalpy independent of salinity. 3: no salinity dependence of thermophysical properties (salt solubility constraints are maintained).
`IE(15)`	I5	allows choice of correlation for brine enthalpy at saturated vapor pressure: 1: after Michaelides (1981). 2: after Miller (1978) (obsolete). 3: after Phillips et al. (1981). 4: after Lorenz et al. (2000) (default = 0). 5: after Driesner (2007).
`IE(16)`	I5	allows choice of the type of NCG (default for `IE(16)` = 0 is CO₂): 1: air. 2: CO₂. 3: CH₄. 4: H₂. 5: N₂.

Table 99 Record **SELEC.2**.#
Parameter	Format	Description
`FE(1)`	E10.4	parameter \(\gamma\) (for `IE(11)` = 1); parameter \(\phi_r\) (for `IE(11)` = 2, 3).
`FE(2)`	E10.4	parameter \(\Gamma\) (for `IE(11)` = 2, 3).