EOS2

This is an updated version of the fluid property module originally developed by OSullivan et al., 1985 for describing fluids in gas-rich geothermal reservoirs, which may contain CO₂ mass fractions ranging from a few percent to occasionally 80% or more (Atkinson et al., 1980). EOS2 accounts for non-ideal behavior of gaseous CO₂, and dissolution of CO₂ in the aqueous phase with heat of solution effects. According to Henry’s law, the partial pressure of a non-condensible gas (NCG) in the gas phase is proportional to the mole fraction of dissolved NCG in the aqueous phase

(49)\[P_{NCG} = K_h x_{aq}^{NCG}\]

The Henry’s law coefficient \(K_h\) for dissolution of CO₂ in water is strongly dependent on temperature. The correlation used in the previous release of EOS2 had been developed by OSullivan et al., 1985 for the elevated temperature conditions encountered in geothermal reservoirs. It is accurate to within a few percent of experimental data in the temperature range of 40˚C ≤ \(T\) ≤ 330˚C, but becomes rather inaccurate at lower temperatures and even goes to negative values for \(T\) < 30˚C (see Figure 7). Subroutine HENRY in EOS2 was replaced with a new routine that uses the correlation developed by Battistelli et al., 1997, which is accurate for 0˚C ≤ \(T\) ≤ 350˚C. The Battistelli et al. formulation agrees well with another correlation that was developed by S. White (1996, private communication).

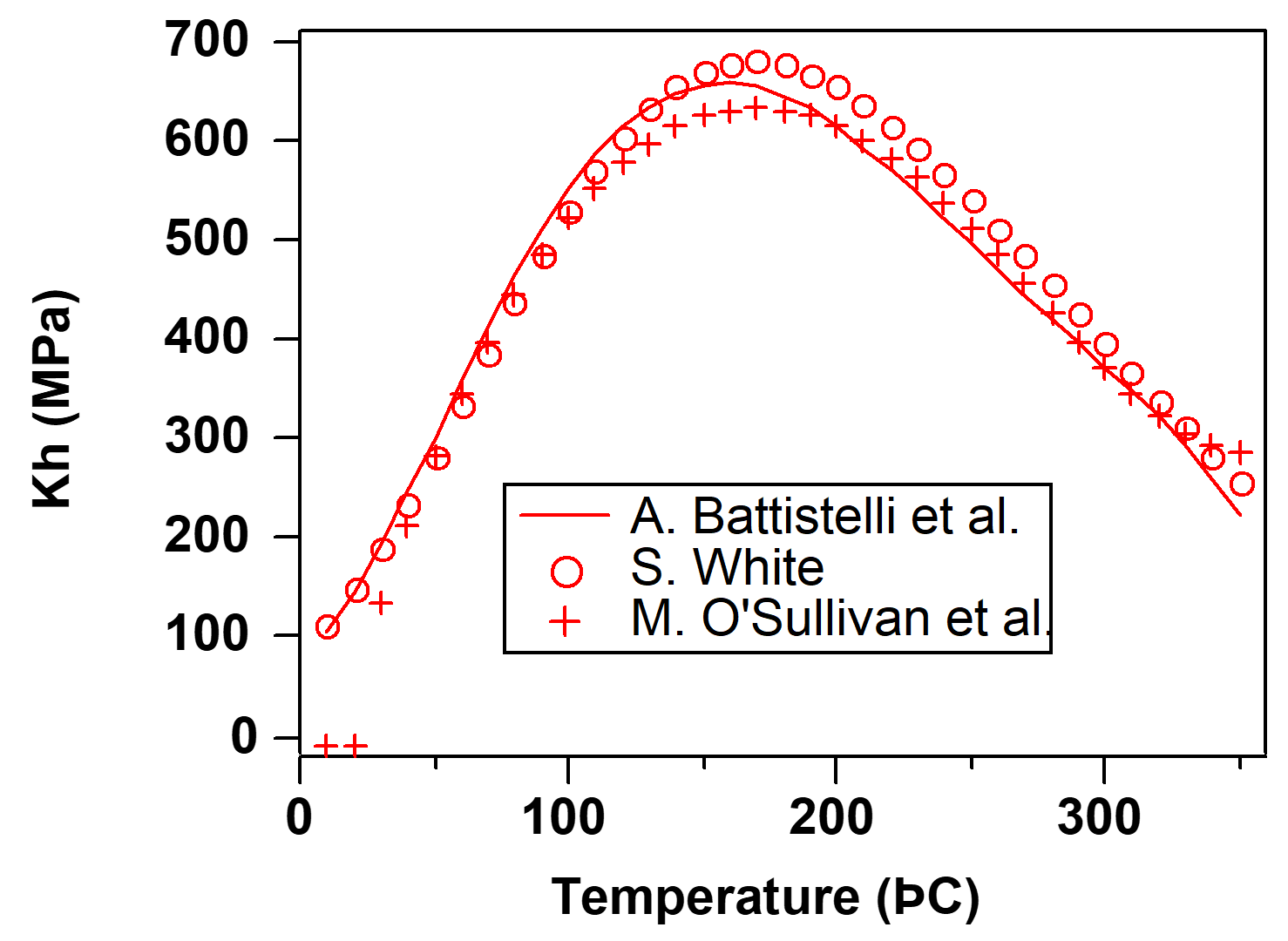
Figure 7 Henry’s law coefficients for dissolution of CO₂ in water.

The viscosity of vapor - CO₂ mixtures is described with a formulation due to Pritchett et al., 1981; other thermophysical property correlations are based on the model of Sutton & McNabb, 1977.

Specifications

A summary of EOS2 specifications and parameters is given in Table 68. A more detailed description and application to geothermal reservoir problems are given in the paper by OSullivan et al., 1985. EOS2 has the parameter settings of (NK, NEQ, NPH, NB) = (2, 3, 2, 6) for solving mass and energy balances for water and CO₂. Molecular diffusion can also be modeled by setting parameter NB equal to 8.

Table 68 Summary of EOS2.

Components	#1: water #2: CO2
Parameter choices	(NK, NEQ, NPH, NB) = (2, 3, 2, 6) Molecular diffusion can be modeled by setting NB = 8
Primary variables	Single-phase conditions: (\(P\), \(T\), \(P_{CO_2}\)): (pressure, temperature, CO2 partial pressure) Two-phase conditions: (\(P_g\), \(S_g\), \(P_{CO_2}\)): (gas phase pressure, gas saturation, CO2 partial pressure)